Gradient Descent

Recall that Cost Function (J),  is a function of our parameters w(weights), and b(bias)...and that cost function tells us how bad we are doing.

So, in order to reduce our cost function, it's only logical to tweak our weights and bias.

Here's a picture that illustrates various costs with respect to different weights and biases (here, for the sake of simplicity, we assume that cost function is a function of only 1 weight and 1 bias)

Image source : https://suniljangirblog.wordpress.com/2018/12/03/the-outline-of-gradient-descent/

Here, x represents the weights, y represents the bias and z represents the Cost

As we can see, our aim through Gradient Descent is to reach lowest Cost, i.e., the lowest point in the z-axis that lies in the convex plane.

This lowest part of the curve/plane is what we call as the "minimum of the graph".

And if you're acquainted with basic calculus, you'd know that there are two types of minima; the local minima and the absolute minima.

We choose the Cost Function in a such a way, so that the curve/plane only has one minima. If it has two or more minima, the gradient descent might get stuck on some local minima and never really reach the global minima (Later on, we'll understand why it happens)

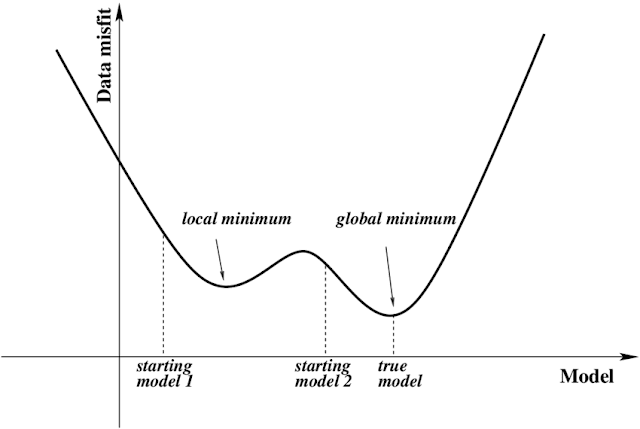Image Source : https://www.researchgate.net/figure/Schematic-of-the-local-minima-problem-in-FWI-The-data-misfit-has-spurious-local-minima_fig1_267820876

This curve, which has more than 1 minima is called as a non-convex function

Curves, which only have 1 minima, are what we call a "Convex Function"

Anyways, going back to Gradient Descent.

What we do in gradient descent is that we start with random values of w and b, and start traversing towards the direction of the minima, like walking down a hill.

Alright now.

Here's what we do in Gradient Descent:

Repeat {

    $w = w - \alpha * \frac{\partial J}{\partial w}$

    $b = b - \alpha * \frac{\partial J}{\partial b}$ 

}

Remember that going down the hill analogy?

Hold on to that!

Let's take the optimization of w first.

We have to go down the hill, right?

That $\frac{\partial J}{\partial w}$ tells us the slope of the curve (Cost Function), with respect to w (how steep the hill is)

and that $\alpha$ is our step size towards the minima.

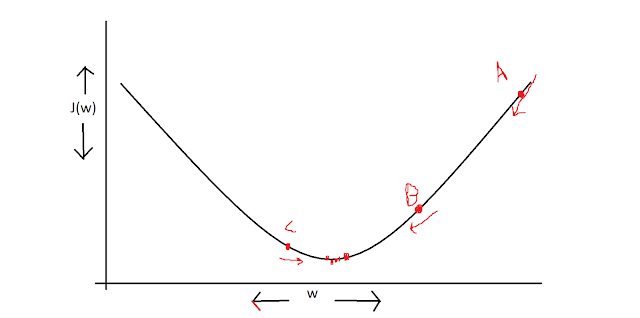
Take this figure:

Suppose we start with random value of w (point A).

At point A, the curve is too steep and also positive. And so, we decrease the value of w (and move till B)

At point B, we would notice that the steepness has reduced quite a bit, so now the step size will be a little smaller (notice that we aren't changing the learning rate $\alpha$....the steepness of the curve is decreasing, hence decreasing the value of $\frac{\partial J}{\partial w}$ and overall the term  $\alpha * \frac{\partial J}{\partial w}$)

If, it overshoots the minima, it might reach to point C. C has a negative slope, therefore, the whole term  $\alpha * \frac{\partial J}{\partial w}$) is now positive and the value of w would be increased very slightly.

Choosing the learning rate is very important because :

Image Source : https://www.jeremyjordan.me/nn-learning-rate/

Now that we know and understand what gradient descent is and how it's calculated and how it works, let's delve further into and try and understand how to calculate the partial differentiations done in the equation.

Doing that, we'll also understand one of the key parts of training a neural network, i.e., Backpropagation 

Previous Post : Logistic Regression

Next Post : Backpropagation (Part 1)