Notations

Before we dive right into the various algorithms of deep learning, we should get acquainted with the common notations used.

Consider this image of a digit

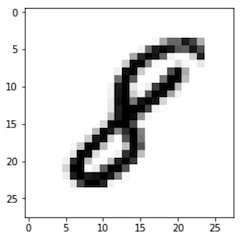Image source : MNIST

This training example contains a 28x28 pixel image along with its correct label, i.e, 8.

Within the computer, this image is stored as a matrix of pixel intensities

Each pixel contains within it, a number from 0-255 representing the intensity of black (with 0 being total absence of black, i.e., white, and 255 being totally black)

Therefore, in the eyes of a computer, this image would be something like this 

If we try to turn these pixel intensity values into a feature vector, what we do is unroll all these pixel intensity values into an input feature vector x.

So we'll take all the pixel values starting from 0, 0, 0....1, 12, 0, 11, 39... until we get a very long feature vector (of size (64x64 =)4096) listing out all the pixel intensities

$$X = \begin{bmatrix} 0 \\ 0 \\ . \\ . \\ . \\ 1 \\ 12 \\ 0 \\ 11 \\ . \\ . \\ 0 \\ 0\end{bmatrix}$$

Therefore, we're going to write n_x = 4096 to represent the dimension of the input feature vector x.

Sometimes for simplification, we might also just use n

So for a classification algorithm, our goal is to an image represented by a feature vector x, and predict the corresponding label y (that lies between 0-9) accurately

A single training example is represented by a pair, i.e., (x,y) where x is an n_x dimensional feature vector and y lies from 0-9

Your training set comprises of m training examples

So your training set will be written as {(x⁽¹⁾, y⁽¹⁾), (x⁽²⁾, y⁽²⁾)....(x^(m),y^(m))} 

...where (x⁽¹⁾, y⁽¹⁾) are the input and output of your 1^st training example and (x⁽²⁾, y⁽²⁾) are the input and output of your 2^nd training example and so on till the last training example (x^(m),y^(m)) where (x^(m),y^(m)) are the input and output of your m^th training example 

and all these all together form your training set.

Sometimes, to emphasize that m is the number of training examples we write it as m_train 

Similarly, we represent the number of test set with m_test

Finally, to put all of the training examples into a more compact notation, we're going to define a matrix X, as defined by taking all your training examples (x⁽¹⁾, x⁽²⁾..and so on) and stacking it column-wise, like so.

$$X = \begin{bmatrix}. & . &  &  &  &  & . \\. & . &  &  &  &  & . \\ . & . &  &  &  &  & . \\x^{(1)} & x^{(2)} & . & . & . & . &  x^{(m)}\\ . & . &  &  &  &  & . \\ . & . &  &  &  &  & . \\ . & . &  &  &  &  & . \end{bmatrix} $$

having m columns where m is the number of training examples

and each training example has n_x rows 

Therefore, X is a n_xxm dimentional  matrix.

X.shape = (n_x, m)

Similarly, we also stack the output y as columns, like 

$$Y = \begin{bmatrix}y^{(1)} & y^{(2)} & . & . & . & . & . &y^{(m)}\end{bmatrix}$$

making it a 1xm dimensional matrix

Y.shape = (1, m).

Previous Post : Plotly

Next Post : Logistic Regression