NumPy

NumPy is a python library used for applying high-level mathematical functions to multi-dimensional arrays and matrices.

In our case it would help us in vectorization.

Vectorization refers to the solution which allow the application of operations to an entire set of arrays at once instead of applying it one element at a time (as is done in case of loops)

Vectorization is much much faster than the traditional loops and most computer can do it more efficiently

(Here is a sample of code to demonstrate just how fast it is)

But before we start with matrices and vectorization and broadcasting and what not, let's start with the very basics and learn how to make and modify matrices

NumPy is usually enabled by default, nevertheless. You can check check it from the Anaconda Navigator

 

(if you don't know about Anaconda Navigator and don't know how to install packages, check the following link)

Now, Open Jupyter notebooks, go to whatever folder you want to save the file in and let's just start now

At first, you need to import NumPy.

we do this by writing

import numpy as np

We usually import NumPy as np, it's not a necessity, just a convention, you can use anything you want though.

Next, let's see how we create a basic array.

We do this by typing in :

np.array([1, 2, 3, 4, 5, 6, 7])

Notice that in case of 2-Dimensional array, there is a square bracket within the square bracket of np.array([ ]).

Visualize it as this format

np.array([[row1], [row2], [row3]])

where each [row] is separated by a comma and each [row] has different elements also separated by commas.

Taking the same approach, you can guess how we make a 3-Dimensional Array

And you can do this forever, nesting a list within a list and keep on making 4-D, 5-D....n-D arrays.

And creating a n-Dimensional array with random values is even simpler!

If you want an array of floats in a particular shape, type in

np.random.rand(shape)

For example:

For creating a 2-D or 3-D array:

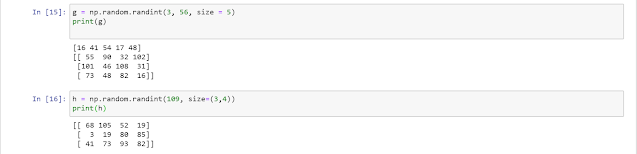
If you instead want to create an array with random numbers, use the code

np.random.randint(<start_number>, <end_number>, size=<size>)

By default, the start number is zero. So if you write

np.random.randint(<end_number>, size=<size>)

Then it'll create an array of random integers from 0-end_number in the shape of <size>.

Here's an example :

Important Note : In Machine Learning, we generally use np.random.randn() rather than np.random.rand()

The diffference between np.random.rand() and np.random.randn() are from the probabilistic distribution each number is drawn from.

np.random.rand() selects numbers from a uniform distribution (from 0 to 1), while np.random.randn() selects numbers from a Normal (a.k.a. Gaussian) distribution.

Here, you can compare both, (select or deselect the labels from the top right to show/hide a distribution)

If you want to create a special kind of a matrix, say a matrix with only zeroes, or only ones, or an identity matrix,

type in 

np.zeros([rows,columns])
np.ones([rows, columns])
np.identity(rows) #because identity matrix always has num_rows = num_columns

If you're given some complex array and you want to find the number of dimension. Use

a.ndim

 

and if you straight up wanna know the dimension, type in 

a.shape

The shape is given in the from of (row, columns). This is very important to remember.

Also, remember that the index starts from 0.

Also, I want you to notice that for a 1-Dimensional vector such as a, a.shape gives the result (5,) and not (5,1) which is what we typically expect.

This is what we call a "Rank-1 Array", and it's a pretty weird array as in it doesn't behave neither as a row vector nor a column vector. It also causes a lot of problems in vector operations and all. I'll give an example down the line.

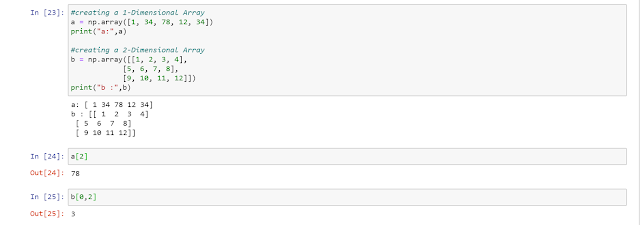
In order to select a particular element, or a particular sub-array from the the whole array, you can simply state the indexing of that element in square brackets like,

a[2] 

or

b[0,2]

And for selecting multiple rows and columns, you can write something like this :

a[:, 3]

or 

b[:,1:3]

And now we encounter our very first problem with rank-1 arrays. There are a lot more problems that these Rank-1 arrays cause, so rather than discussing what they are, and why they are causing such errors, let's shift our focus on how to correct them (because that's easy)

There are 2 ways:

1. You reshape the already existing Rank-1 array
2. You specify the shape while creating (recommended)

Also, changing a number in an array is just as easy, just type in 

b[row, column] = new_number

And if you want to change a part of the array, write a new array and then select the part to be changed and assign it to that newly created array

As a rule of thumb, we want to avoid for loops as much as possible.

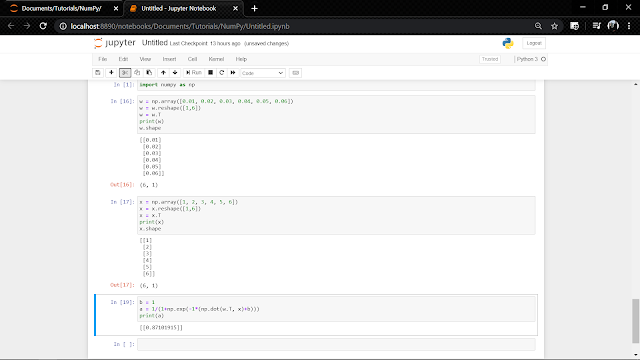
So then, suppose we have some operation that we want to perform on all the elements of the matrix (as in case of applying the sigmoid function in logistic)

For example, in logistic regression, we needed to compute $z = w^Tx+b$ where w and x are both $n_x$ dimensional vector$$w = \begin{bmatrix}1 \\ 2 \\ . \\ . \\ . \\ n \end{bmatrix}    x = \begin{bmatrix}1 \\ 2 \\ . \\ . \\ . \\ n \end{bmatrix}$$

we do this matrix multiplication, with the following command

z = np.dot(w.T, x)

where w.T is the transpose of the matrix w and np.dot(w.T, x) multiplies the matrix w.T with x

now we add b to z, and then take the sigmoid of the entire thing

therefore, 

Or, in one line, you can type it as

b = 1
a = 1/(1+np.exp(-1*(np.dot(w.T, x)+b)))

np.exp() is just one of the several functions you can apply over an entire array.

There are also np.log(), np.sin(), np.abs() 

Like..

There's also 

np.max(array, axis)

that tells you the maximum in each column (if axis =0) and maximum in each row (if axis = 1)

And finally at last, there's just one last concept that we want to get acquainted ourselves with.

Broadcasting

Let me just directly show what broadcasting does.

If try and add a constant to an array, observe what happens

What it's doing is that, internally, it takes 10, and makes it a 5x1 array and then adds each element of that array with a.

Similarly, we can add/subtract/divide/multiply different arrays/numbers with another array

And 

The End

We've covered the basics of NumPy, we'd be using all of these in all of our future projects.

NumPy is a very essential tool, so I suggest practicing all of the functions in your own computer as well.

I hope all the explanations were clear. 

If not, do comment your questions/suggestion.

Cheers!

Satwik

Previous Post : Intro to Pandas

Next Post : Plotly